Sponsored Links
データの読み込みと準備
データ指向統計データベースの中の新国民生活指標(住む)データ[1]を使わせていただきます。このデータは47都道府県別の様々な変数(23変数)がまとめられています。借家の1畳当たり実質家賃を他の変数を使って予測するための重回帰分析を行います。
> x <- read.table(pipe("pbpaste"), header=TRUE) # クリップボードからデータを読み込み、xに代入。ちなみにこちらはMac用のコードでWindowsは、read.table("clipboard", header=TRUE)。
重回帰分析(全ての変数を強制投入)
まずはすべての変数を強制投入して重回帰分析を実行してみます。
> regx <- lm(x$Rent ~ ., data=x) # Rentを目的変数に設定。「~」の右辺に説明変数を記載する。今回はRent以外の全ての変数を説明変数に設定するので「.」として省略できる。
> summary(regx) # regxの結果を表示。
Call:
lm(formula = x$Rent ~ ., data = x)
Residuals:
Min 1Q Median 3Q Max
-289.20 -108.55 -12.55 127.01 288.72
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 6981.1067 4075.1768 1.713 0.09959 .
NonRep 1.4653 33.6592 0.044 0.96564
OverMin -110.2071 36.4576 -3.023 0.00588 **
HomeOwn -1.4271 10.5136 -0.136 0.89316
CompPol 0.7447 3.6063 0.206 0.83815
NumClime 50.5615 19.2329 2.629 0.01471 *
NumLarc -1.1765 0.7485 -1.572 0.12911
TrafAcci 0.1145 0.3414 0.335 0.74029
Fire 2.2725 4.0299 0.564 0.57805
DspRubb -3.1819 7.2426 -0.439 0.66435
Sidewalk 8.9887 19.4323 0.463 0.64784
MedFacil 4.6499 7.5337 0.617 0.54290
OverOrd -42.5344 44.2588 -0.961 0.34612
Sunshine 2.9958 12.3768 0.242 0.81080
NumMat 392.7490 257.6219 1.525 0.14045
AreaResi 1.6584 1.2344 1.344 0.19168
Transpt 6.6152 9.2422 0.716 0.48104
AreaPark -16.7993 13.9994 -1.200 0.24185
Sewarage 3.3871 4.8042 0.705 0.48757
Recycle 32.2740 16.5976 1.944 0.06365 .
AmtRubb 0.1561 0.2602 0.600 0.55405
AvgMin 23.2457 11.8467 1.962 0.06143 .
Pavement 0.3814 5.5734 0.068 0.94601
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 198.7 on 24 degrees of freedom
Multiple R-squared: 0.9354, Adjusted R-squared: 0.8763
F-statistic: 15.81 on 22 and 24 DF, p-value: 1.833e-09F値の有意確率からみたp値は非常に小さく、Adjusted R2(自由度調整済み決定係数)が0.8763と高いですが、有意な説明変数はOverMin(最低居住水準以上住宅比率)、NumClime(重要刑法犯罪認知件数)だけでした。
上の表のInterceptは切片を表し、Estimateが偏回帰係数を表します。
Rent = 6981.1067 + 1.4653 * NonRep + (-110.2071) * OverMin +…..
という計算式でRentを予測できます。
重回帰分析(全ての変数を強制投入)モデル式の標準偏回帰係数
偏回帰係数は、独立変数・従属変数 単位に依存するため、単位が異なる場合は標準化した標準偏回帰係数(β)を計算して、利用します。
標準偏回帰係数=偏回帰係数×(独立変数 SD/従属変数 SD)
で計算できるらしいので、以下のコマンドで計算できます。
> s <- sapply(x, sd) # データxの全ての変数の標準偏差を計算
> coe <- coefficients(regx)[-1] # 重回帰モデルregxの偏回帰係数をcoefficients関数を使って取りだす。偏回帰係数の1列目は切片なので、「-」を付けて1列目を削除と指定。
> beta <- coe*s[-3]/s[3] # sの3列目が目的変数のRent
> beta
NonRep OverMin HomeOwn CompPol NumClime NumLarc
0.003220532 -0.657757343 -0.022002773 0.016354969 0.232994714 -0.150533623
TrafAcci Fire DspRubb Sidewalk MedFacil OverOrd
0.027214875 0.042694686 -0.053914090 0.070296307 0.101084664 -0.671373442
Sunshine NumMat AreaResi Transpt AreaPark Sewarage
0.040700015 0.849494162 0.191850113 0.076225539 -0.110592441 0.105639914
Recycle AmtRubb AvgMin Pavement
0.223752025 0.068389102 0.275875706 0.008227586 ちなみにscale関数を使って変数を全て標準化してから重回帰分析を行って得られる偏回帰係数も標準偏回帰係数であり、上述の計算方法で得られる値と一致します。
> z <- scale(x) # scale関数を用いて、平均値を引いて標準偏差で割った値に標準化。
> z <- as.data.frame(z) # matrix型になっているので、data.frame型に戻す。
> regz <- lm(z$Rent ~ ., data=z) # 標準化した変数を使って重回帰分析。
> coefficients(regz) # 編回帰係数=標準編回帰係数βを取り出す。
(Intercept) NonRep OverMin HomeOwn CompPol NumClime
-6.621892e-16 3.220532e-03 -6.577573e-01 -2.200277e-02 1.635497e-02 2.329947e-01
NumLarc TrafAcci Fire DspRubb Sidewalk MedFacil
-1.505336e-01 2.721487e-02 4.269469e-02 -5.391409e-02 7.029631e-02 1.010847e-01
OverOrd Sunshine NumMat AreaResi Transpt AreaPark
-6.713734e-01 4.070001e-02 8.494942e-01 1.918501e-01 7.622554e-02 -1.105924e-01
Sewarage Recycle AmtRubb AvgMin Pavement
1.056399e-01 2.237520e-01 6.838910e-02 2.758757e-01 8.227586e-03 重回帰分析(全ての変数を強制投入)モデル式の多重共線性を確認
目的変数同士に強い相関があるときに生じる現象を多重共線性と言います。多重強制性が高いモデル式は良くないそうです。多重共線性の指標としてVIF(Variance Inflation Factor)が用いられ、一般的に10以上は多重共線性が高いと判断するようです。パッケージcarにあるvif関数を使います。
> library(car) # パッケージcarを読み込む。
> vif(regx) # regxで定めた重回帰モデルのVIFを計算する。
NonRep OverMin HomeOwn CompPol NumClime NumLarc TrafAcci Fire DspRubb Sidewalk
2.034729 17.603336 9.768555 2.332466 2.920424 3.410566 2.448860 2.131273 5.599252 8.586608
MedFacil OverOrd Sunshine NumMat AreaResi Transpt AreaPark Sewarage Recycle AmtRubb
9.972349 181.447749 10.512027 115.441588 7.581491 4.216651 3.157877 8.347080 4.922940 4.828373
AvgMin Pavement
7.349216 5.374412
VIFが10以上の変数がいくつかあります。説明変数に全部強制投入しただけあって良いモデルとは言えませんね。
重回帰分析(全ての変数を強制投入)モデル式の情報量基準
モデル式の適合度を評価する指標に情報量基準があり、有名なのがAIC(赤池情報量規準)やBIC(ベイジアン情報量規準)です。この数値が低いほど良いモデルらしいですが、どれくらいの数値以下が良いという絶対的な決まりはないようです。AICとBICはRで簡単に計算できます。
> extractAIC(regx) # AICを計算する関数。説明変数の数、AICの順に表示される。
[1] 23.0000 511.8405
重回帰分析(ステップワイズ法)
step関数を使います。ステップワイズ選択法には増加法、減少法、増減法とありますが、何も設定しないと増減法に設定されているようです。
step(重回帰モデル, direction=”forward”)
と設定すると増加法が指定されます。”backward”で減少法、デフォルトは”both”で増減法になっています。step関数はAICを指標にして良いモデルを探します。
> step(regx) # 重回帰モデルregxの説明変数をステップワイズ法にて選択。
〜〜〜〜〜(途中 略)〜〜〜〜〜
Step: AIC=493.7
x$Rent ~ OverMin + NumClime + NumLarc + MedFacil + NumMat + AreaResi +
AreaPark + Recycle + AmtRubb + AvgMin
Df Sum of Sq RSS AIC
1073471 493.70
- AreaPark 1 55071 1128542 494.06
- AmtRubb 1 82400 1155870 495.18
- AreaResi 1 102071 1175541 495.97
- MedFacil 1 123890 1197361 496.84
- NumLarc 1 154125 1227596 498.01
- Recycle 1 226645 1300116 500.71
- AvgMin 1 372770 1446241 505.71
- NumMat 1 414307 1487778 507.04
- NumClime 1 579777 1653248 512.00
- OverMin 1 1287784 2361254 528.75
Call:
lm(formula = x$Rent ~ OverMin + NumClime + NumLarc + MedFacil +
NumMat + AreaResi + AreaPark + Recycle + AmtRubb + AvgMin,
data = x) # これがステップワイズ法により得られた重回帰モデル。
Coefficients:
(Intercept) OverMin NumClime NumLarc MedFacil NumMat AreaResi AreaPark
10034.4767 -127.1426 57.5982 -1.1576 9.5025 136.2044 1.3803 -11.7015
Recycle AmtRubb AvgMin
28.7033 0.2326 24.4414
> stepregx <- lm(formula = x$Rent ~ OverMin + NumClime + NumLarc + MedFacil + NumMat + AreaResi + AreaPark + Recycle + AmtRubb + AvgMin, + data = x) # ステップワイズ法で得られた重回帰モデルをstepregxに代入。
> summary(stepregx) # stepregxの結果を表示。
Call:
lm(formula = x$Rent ~ OverMin + NumClime + NumLarc + MedFacil +
NumMat + AreaResi + AreaPark + Recycle + AmtRubb + AvgMin,
data = x)
Residuals:
Min 1Q Median 3Q Max
-265.07 -117.45 6.67 102.59 329.93
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 10034.4767 1750.2921 5.733 1.58e-06 ***
OverMin -127.1426 19.3470 -6.572 1.21e-07 ***
NumClime 57.5982 13.0624 4.409 8.98e-05 ***
NumLarc -1.1576 0.5092 -2.273 0.029062 *
MedFacil 9.5025 4.6619 2.038 0.048915 *
NumMat 136.2044 36.5404 3.727 0.000662 ***
AreaResi 1.3803 0.7461 1.850 0.072514 .
AreaPark -11.7015 8.6104 -1.359 0.182602
Recycle 28.7033 10.4112 2.757 0.009103 **
AmtRubb 0.2326 0.1399 1.662 0.105130
AvgMin 24.4414 6.9127 3.536 0.001139 **
---
Signif. codes: 0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1
Residual standard error: 172.7 on 36 degrees of freedom
Multiple R-squared: 0.9269, Adjusted R-squared: 0.9066
F-statistic: 45.63 on 10 and 36 DF, p-value: < 2.2e-16
重回帰分析(ステップワイズ法)モデル式の多重共線性を確認
いずれの説明変数もVIFが10を下回っており、問題となる多重共線性はなくなりました。
> library(car) # パッケージcarを呼び出す。
> vif(stepregx) # ステップワイズ法で得られた重回帰モデル式stepregxのVIFを確認。
OverMin NumClime NumLarc MedFacil NumMat AreaResi AreaPark Recycle AmtRubb AvgMin
6.563771 1.783653 2.089501 5.056081 3.075053 3.667111 1.581708 2.564763 1.848749 3.313263
重回帰分析(ステップワイズ法)モデル式の情報量基準
ステップワイズ法の途中にも出てきましたが、一応AICを確認します。AIC=493.7042ということで、全部投入のモデル511.8405より下がりました。
> extractAIC(stepregx) # AICを計算。
[1] 11.0000 493.7042
重回帰分析(ステップワイズ法)モデル式の評価
predict関数を使って説明変数から得られる予測値を計算できます。
> predict(stepregx)
1 2 3 4 5 6 7 8 9 10 11 12
1632.031 1295.230 1719.676 2033.024 1689.347 1522.580 1646.870 2185.741 2143.926 1774.274 3036.778 2890.107
13 14 15 16 17 18 19 20 21 22 23 24
4140.844 3200.020 1807.071 1852.402 1915.923 1670.528 2175.826 2026.047 1751.588 2271.640 2115.272 1692.369
25 26 27 28 29 30 31 32 33 34 35 36
1823.184 2722.645 2963.842 2501.174 2246.087 1787.148 1848.257 1454.926 1740.943 1781.573 1627.623 1852.881
37 38 39 40 41 42 43 44 45 46 47
1661.882 1511.199 1675.082 2163.284 1579.402 1949.072 1747.334 1597.721 1523.063 1343.068 2144.495 重回帰分析の実測値と予測値の関係をグラフで書きます。
> plot(x$Rent, predict(stepregx), xlim=c(1200, 5000), ylim=c(1200, 5000)) # x$rent(実測値)とpredict(stepregx)(予測値)の散布図を書く。xlimでx軸の目盛り範囲を、ylimでy軸の目盛り範囲を指定。
> abline(1, 1) # xyの勾配比1:1の直線を書く。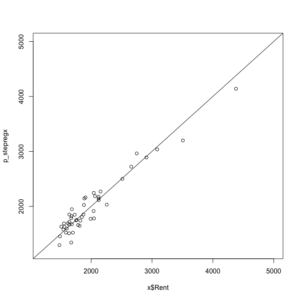
ステップワイズ法で得られた重回帰モデルで選択された10の説明変数を用いて予測される目的変数Rentの予測値とRentの実測値との差(残差)を得るにはresiduals関数を用います。
> residuals(stepregx)
1 2 3 4 5 6 7 8 9
-122.031043 184.770005 -76.676321 223.976199 -135.347093 178.420071 164.130248 -122.740639 -20.925726
10 11 12 13 14 15 16 17 18
217.725792 48.222456 17.892925 238.156318 306.980059 39.928586 21.597618 125.076824 -30.527977
19 20 21 22 23 24 25 26 27
-52.825694 -145.046784 9.411848 -116.640264 9.727938 -72.368755 -146.184143 -63.644545 -213.842273
28 29 30 31 32 33 34 35 36
12.825929 -203.087114 -114.148037 -118.257247 34.074425 81.056652 265.426994 -65.622627 -210.880816
37 38 39 40 41 42 43 44 45
124.118264 127.800519 8.917511 -255.284396 -35.401787 -265.072426 6.666265 1.279178 63.936903
46 47
329.931644 -255.495464 視覚的に確認するためにはplot関数を使ってグラフを書きます。
> par(mfrow=c(2,2)) # par関数はグラフィックスのパラメータを設定する関数。因数mfrowで2行×2列で並べる指示。
> plot(stepregx)◆Residuals vs Fitted:残差と予測値のプロット
グラフの横軸が予測値、縦軸が残差である。予測値が20,000円近辺の残差が大きいことがわかる。
◆Normal Q−Q:残差の正規Q-Qプロット
横軸は標準正規分布の分位点、横軸は標準化した残差。通常の回帰分析は残差が正規分布に従う過程で計算されており、データの正規性を確認するグラフ。
◆Scale−Location:残差の平方根プロット
標準化した残差の平方根を縦軸に、予測値を横軸にとったグラフ。残差の変動を確認するグラフ。
◆Residuals vs Leverage:Cookの距離のプロット
Cookの距離は回帰分析の影響力の大きいデータを検出するのに役立ち、Cookの距離が大きいと回帰式に大きな影響を与えるデータと言える。通常Cookの距離が0.5以上は大きな影響を与えるデータとみなす。今回の回帰式では全て0.5以内(赤い点線の範囲内)に収まっている。
重回帰分析(ステップワイズ法)をBland-Altman分析で評価
Bland-Altman分析は、2つの手法の誤差の許容範囲95%を示すことによって、誤差の程度を評価する手法だそうです[1],[2],[3]。RではパッケージBlandAltmanLehを使い、Bland-Altmanの統計量を計算し、グラフを作ることができます。
> library(BlandAltmanLeh) # パッケージBlandAlmanLehを読み込む。
> bland.altman.stats(x$Rent, predict(stepregx)) # Bland-Altman統計量を計算。
$means # Rentの実測値と予測値の平均値(足して2で割った値)
[1] 1571.016 1387.615 1681.338 2145.012 1621.674 1611.790 1728.935 2124.370 2133.463
[10] 1883.137 3060.889 2899.054 4259.922 3353.510 1827.036 1863.201 1978.462 1655.264
〜〜〜〜〜(以下略、47まである)〜〜〜〜〜
$diffs # Rentの実測値と予測値の差
[1] -122.031043 184.770005 -76.676321 223.976199 -135.347093 178.420071 164.130248
[8] -122.740639 -20.925726 217.725792 48.222456 17.892925 238.156318 306.980059
〜〜〜〜〜(以下略、47まである)〜〜〜〜〜
$groups # Bland-Altman plotを書くためのデータ。
group1 group2
1 1510 1632.031
2 1480 1295.230
3 1643 1719.676
4 2257 2033.024
5 1554 1689.347
〜〜〜〜〜(以下略、47まである)〜〜〜〜〜
$based.on # ?
[1] 47
$lower.limit # 許容範囲の下限。(多分)
[1] -299.4141
$mean.diffs # 差の平均?
[1] -1.132036e-12
$upper.limit # 許容範囲の下限。(多分)
[1] 299.4141
$lines # ?
lower.limit mean.diffs upper.limit
-2.994141e+02 -1.132036e-12 2.994141e+02
$CI.lines
lower.limit.ci.lower lower.limit.ci.upper mean.diff.ci.lower mean.diff.ci.upper # 許容範囲の下限の95%信頼区間下限 許容範囲の下限の95%信頼区間上限 差の平均の95%信頼区間下限 差の平均の95%信頼区間上限
-377.1013 -221.7270 -44.8527 44.8527
upper.limit.ci.lower upper.limit.ci.upper # 許容範囲の上限の95%信頼区間下限 許容範囲の上限の95%信頼区間上限
221.7270 377.1013
$two # ?
[1] 1.96
$critical.diff # ?
[1] 299.4141日本語のページが見当たらなくてよく分からないので、詳しい人がいたら教えて欲しいです。
グラフは以下のようにして書きます。これをみるとほぼ許容範囲内に収まっているので、それなりのモデル式になったことが伺えます。
> bland.altman.plot(x$Rent, predict(stepregx), main="Bland Altman Plot", xlab="Means", ylab="Differences", conf.int=.95)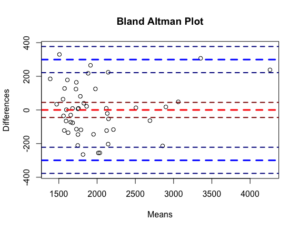
Sponsored Links


