偏最小二乗回帰（PLS回帰）分析

データの読み込みと準備

重回帰分析で利用したデータ指向統計データベースの中の新国民生活指標（住む）データ[1]を使わせていただきます。このデータは47都道府県別の様々な変数（23変数）がまとめられています。借家の1畳当たり実質家賃を他の変数を使って予測するためのPLS回帰分析を行います。

[1] データ指向統計解析環境 DoSS – DATA] PLIlive

PLS回帰分析

パッケージplsの中にあるplsrという関数を使います。

plsr(目的変数 ~ 従属変数, 潜在変数の数, data=データ名, validation = “CVもしくはLOO”, scale=TRUEもしくはFALSE)

という式になります[1]。validationは変数選択の方法で、CV（cross-validation）とLOO（leave-one-out cross-validation ）があります。scaleがTRUEなら各変数を標本標準偏差で割でデータを正規化します。潜在変数の数は説明変数の数より多いとエラーが出ます。最初は説明変数の数と同數の数字を入れておいて、潜在変数が1から説明変数の数までのRMSEP（平方平均二乗誤差；root m- ean squared error of prediction）を見て、どの潜在変数の数が最適なモデルか判断します。RMSEPは小さいほど良いモデルとされています。

まずはvalidationをCVに設定した結果から。

R Console

> plscv <- plsr(x$Rent ~ ., 22, data=x, validation = "CV", scale=TRUE) # plsvbに代入。 
> summary(plscv) # plsvbの結果を表示。
Data: 	X dimension: 47 22 
	Y dimension: 47 1
Fit method: kernelpls
Number of components considered: 22

VALIDATION: RMSEP
Cross-validated using 10 random segments.
       (Intercept)  1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps
CV             571    327.8    317.6    333.0    344.7    377.6    376.8    369.3
adjCV          571    325.8    313.3    325.4    335.2    364.1    363.4    356.6
       8 comps  9 comps  10 comps  11 comps  12 comps  13 comps  14 comps  15 comps
CV       353.9    355.8     355.8     354.0     351.1     346.0     346.4     344.8
adjCV    342.4    344.2     344.2     342.5     339.9     335.1     335.6     334.1
       16 comps  17 comps  18 comps  19 comps  20 comps  21 comps  22 comps
CV        343.6     341.6     348.9     349.2     347.6     348.0     348.0
adjCV     333.0     331.0     337.7     338.0     336.5     336.9     336.9

TRAINING: % variance explained
        1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps
X         39.76    52.60    60.52    64.82    66.90    71.55    75.25    80.19    82.96
x$Rent    74.87    83.44    88.04    90.22    91.99    92.45    92.81    92.97    93.13
        10 comps  11 comps  12 comps  13 comps  14 comps  15 comps  16 comps  17 comps
X          85.46     87.01     89.67     91.35     93.55     94.81     95.96     97.06
x$Rent     93.21     93.28     93.30     93.33     93.34     93.36     93.41     93.48
        18 comps  19 comps  20 comps  21 comps  22 comps
X          97.79     98.55     99.35     99.67    100.00
x$Rent     93.53     93.54     93.54     93.54     93.54
> plot(plscv, "validation") # RMSEPのグラフを表示。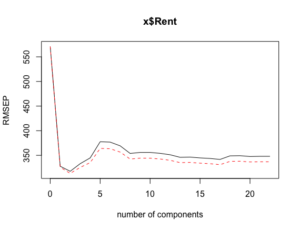

潜在変数が2の時にRMSEPが最小になっています。

次にvalidationをLOOに設定した結果です。

R Console

> plsloo <- plsr(x$Rent ~ ., 22, data=x, validation = "LOO", scale=TRUE) # plsvbに代入。
> summary(plsloo) # plsvbの結果を表示。
Data: 	X dimension: 47 22 
	Y dimension: 47 1
Fit method: kernelpls
Number of components considered: 22

VALIDATION: RMSEP
Cross-validated using 47 leave-one-out segments.
       (Intercept)  1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps
CV             571    322.3    311.8    317.5    319.3    340.0    338.5    333.6
adjCV          571    322.0    310.9    316.1    317.7    337.6    336.3    331.4
       8 comps  9 comps  10 comps  11 comps  12 comps  13 comps  14 comps  15 comps
CV       326.8    330.5     333.7     332.8     334.1     333.6     331.5     330.8
adjCV    324.8    328.4     331.6     330.7     331.9     331.4     329.4     328.7
       16 comps  17 comps  18 comps  19 comps  20 comps  21 comps  22 comps
CV        328.8     328.2     332.6     332.7     333.0     333.5     333.6
adjCV     326.8     326.1     330.5     330.6     330.9     331.4     331.4

TRAINING: % variance explained
        1 comps  2 comps  3 comps  4 comps  5 comps  6 comps  7 comps  8 comps  9 comps
X         39.76    52.60    60.52    64.82    66.90    71.55    75.25    80.19    82.96
x$Rent    74.87    83.44    88.04    90.22    91.99    92.45    92.81    92.97    93.13
        10 comps  11 comps  12 comps  13 comps  14 comps  15 comps  16 comps  17 comps
X          85.46     87.01     89.67     91.35     93.55     94.81     95.96     97.06
x$Rent     93.21     93.28     93.30     93.33     93.34     93.36     93.41     93.48
        18 comps  19 comps  20 comps  21 comps  22 comps
X          97.79     98.55     99.35     99.67    100.00
x$Rent     93.53     93.54     93.54     93.54     93.54
> plot(plsloo, "validation") # RMSEPのグラフを表示。

LOOでも潜在変数が2の時にRMSEPが最小になっています。

RMSEPはCVで313.3、LOOで310.9となり、若干LOOの方が小さいので、以下validationをLOOにして、潜在変数が2と設定して計算します。

MEMO

潜在変数は2つでも、その中には元々の説明変数22個が含まれています。全ての変数を無駄にせず計算に組み込むという点において意義があるのかもしれません。

[1] The Comprehensive R Archive Network – Package ‘pls’

PLS回帰分析の評価

まずはPLS回帰モデルのR²を計算します。

R Console

> R2(plsloo) # パッケージplsに含まれているR2関数で、それぞれの潜在変数におけるR²を計算できる。
(Intercept)      1 comps      2 comps      3 comps      4 comps      5 comps  # 潜在変数が2で最大。
   -0.04395      0.66739      0.68882      0.67723      0.67359      0.62996  
    6 comps      7 comps      8 comps      9 comps     10 comps     11 comps  
    0.63305      0.64369      0.65800      0.65021      0.64343      0.64534  
   12 comps     13 comps     14 comps     15 comps     16 comps     17 comps  
    0.64262      0.64371      0.64808      0.64962      0.65381      0.65510  
   18 comps     19 comps     20 comps     21 comps     22 comps  
    0.64574      0.64551      0.64487      0.64380      0.64377

潜在変数が2の時の各説明変数の係数を計算します。

R Console

> plsloo$coefficients[,,2] # 説明変数を計算。[,,2]で潜在変数が2の時のデータを指定。
     NonRep     OverMin     HomeOwn     CompPol    NumClime     NumLarc    TrafAcci 
-11.8630683 -66.5232974 -37.4490988  40.1409648  89.4600896  32.8865007  21.3376944 
       Fire     DspRubb    Sidewalk    MedFacil     OverOrd    Sunshine      NumMat 
 -3.8790425  54.2653131   7.8153827  41.2184634 -29.3533977 -35.2151926 -23.0802366 
   AreaResi     Transpt    AreaPark    Sewarage     Recycle     AmtRubb      AvgMin 
 -0.7974459  19.5292946 -50.7619888  70.3953091  73.6767582  -2.9313300  99.1595406 
   Pavement 
 20.3463467

次にpredict関数で、PLS回帰モデルによる予測値を計算します。

R Console

> predict(plsloo)[,,2] # 予測値を計算。[,,2]で潜在変数が2の時のデータを指定。
       1        2        3        4        5        6        7        8        9 
1461.367 1184.229 1444.983 2090.417 1261.183 1540.853 1668.437 2129.942 2063.041 
      10       11       12       13       14       15       16       17       18 
1909.182 3020.408 2933.528 3568.376 3217.177 1680.277 1734.847 1691.910 1755.526 
      19       20       21       22       23       24       25       26       27 
2028.064 1837.905 1846.844 2264.669 2342.794 1645.778 2010.502 2718.861 3153.245 
      28       29       30       31       32       33       34       35       36 
2215.345 2269.342 1839.868 1872.854 1387.413 1799.348 2074.900 1746.283 1689.286 
      37       38       39       40       41       42       43       44       45 
1688.154 1858.921 1756.933 2466.798 1769.636 1869.195 1803.537 1732.396 1669.291 
      46       47 
1521.462 2199.694

Bland-Altman分析で評価します。

R Console

> bland.altman.stats(x$Rent, predict(plsloo)[,,2])
$means
 [1] 1485.683 1332.114 1543.992 2173.708 1407.592 1620.926 1739.718 2096.471 2093.021
[10] 1950.591 3052.704 2920.764 3973.688 3362.088 1763.638 1804.423 1866.455 1697.763
[19] 2075.532 1859.452 1803.922 2209.835 2233.897 1632.889 1843.751 2688.931 2951.622
[28] 2364.673 2156.171 1756.434 1801.427 1438.207 1810.674 2060.950 1654.142 1665.643
[37] 1737.077 1748.961 1720.466 2187.399 1656.818 1776.598 1778.768 1665.698 1628.145
[46] 1597.231 2044.347

$diffs
 [1]   48.63315  295.77131  198.01677  166.58338  292.81698  160.14720  142.56311
 [8]  -66.94236   59.95895   82.81766   64.59207  -25.52766  810.62377  289.82316
[15]  166.72333  139.15341  349.08961 -115.52594   94.93649   43.09537  -85.84440
[22] -109.66912 -217.79447  -25.77758 -333.50217  -59.86114 -403.24460  298.65481
[29] -226.34236 -166.86753 -142.85385  101.58698   22.65172  -27.90000 -184.28332
[36]  -47.28609   97.84559 -219.92116  -72.93254 -558.79781 -225.63597 -185.19522
[43]  -49.53667 -133.39603  -82.29076  151.53766 -310.69371

$groups
   group1   group2
1    1510 1461.367
2    1480 1184.229
3    1643 1444.983
4    2257 2090.417
5    1554 1261.183
6    1701 1540.853
7    1811 1668.437
8    2063 2129.942
9    2123 2063.041
10   1992 1909.182
11   3085 3020.408
12   2908 2933.528
13   4379 3568.376
14   3507 3217.177
15   1847 1680.277
16   1874 1734.847
17   2041 1691.910
18   1640 1755.526
19   2123 2028.064
20   1881 1837.905
21   1761 1846.844
22   2155 2264.669
23   2125 2342.794
24   1620 1645.778
25   1677 2010.502
26   2659 2718.861
27   2750 3153.245
28   2514 2215.345
29   2043 2269.342
30   1673 1839.868
31   1730 1872.854
32   1489 1387.413
33   1822 1799.348
34   2047 2074.900
35   1562 1746.283
36   1642 1689.286
37   1786 1688.154
38   1639 1858.921
39   1684 1756.933
40   1908 2466.798
41   1544 1769.636
42   1684 1869.195
43   1754 1803.537
44   1599 1732.396
45   1587 1669.291
46   1673 1521.462
47   1889 2199.694

$based.on
[1] 47

$lower.limit
[1] -450.6015

$mean.diffs
[1] 0

$upper.limit
[1] 450.6015

$lines
lower.limit  mean.diffs upper.limit 
  -450.6015      0.0000    450.6015 

$CI.lines
lower.limit.ci.lower lower.limit.ci.upper   mean.diff.ci.lower   mean.diff.ci.upper 
           -567.5163            -333.6867             -67.5008              67.5008 
upper.limit.ci.lower upper.limit.ci.upper 
            333.6867             567.5163 

$two
[1] 1.96

$critical.diff
[1] 450.6015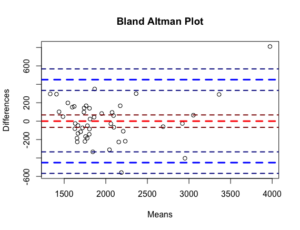

重回帰分析のBland-Altman Plotと見比べていただければ一目瞭然ですが、重回帰分析の方が精度いいんですよね。

注意

PLS回帰分析は正直ここに記載した方法であっているのかどうか不安な部分もあるので、間違っていたらご意見ください。ちなみに、今回は22変数全てを投入しましtが、ステップワイズ法で選択された変数だけを投入した方がR²もRSEPもよくなるので、変数選択をどのようにするかも考えないといけないのかもしれません。

データの読み込みと準備

PLS回帰分析

PLS回帰分析の評価

コメントを残す コメントをキャンセル

コメントを残すコメントをキャンセル