Rでデータを生成

データ生成の基本

自分で数を打ち込む

c()の中に数値を打ち込み、ベクトルを作成します。複数のベクトルを合わせることもできます。

R Console

> x <- c(1,2,3,4) 
> y <- c(x,5,6,7) 
> z <- c(y,8,9) 
> z
[1] 1 2 3 4 5 6 7 8 9

同じものを繰り返す

rep関数を使って同じものを繰り返して生成します。以下にいくつか例を示します。

R Console

> rep(7, times=3) # オプションtimesで繰り返す回数を指定。
[1] 7 7 7
> rep(c(1,2,3), times=2) # ベクトルも繰り返すことができる。 
[1] 1 2 3 1 2 3
> rep(c(3,2,1), each=3) # オプションeachで繰り返す回数を指定すると、一つずつ繰り返す。 
[1] 3 3 3 2 2 2 1 1 1
> rep(c(1,2,3), length=10) # オプションlengthで生成するデータの長さを指定。 
 [1] 1 2 3 1 2 3 1 2 3 1
> rep(c(7,8,9), times=c(2,1,3)) # オプションtimesはベクトルとしても指定できる。この例では7を2つ、8を1つ、9を3つ生成。 
[1] 7 7 8 9 9 9
> rep(c("fair","good","normal"), times=c(2,3,1)) # 文字列も繰り返し生成できる。 
[1] "fair"   "fair"   "good"   "good"   "good"   "normal"
> rep(paste("patient", c(1:5), sep="_"), times=2) # paste関数と組み合わせるとこのようなこともできる。
 [1] "patient_1" "patient_2" "patient_3" "patient_4" "patient_5" "patient_1" "patient_2"
 [8] "patient_3" "patient_4" "patient_5"

MEMO

paste関数は2つの文字列をつなぎ合せる。また、オプションsepは2つの文字列の間に挟む文字列を指定できる。

> paste(“I”, “lunch.”, sep = ” eat “)
[1] “I eat lunch.”

等差数列を作る

順に1ずつ増やしたり減したりする整数を生成するには「：」を数字で囲む。

R Console

> 1:5
[1] 1 2 3 4 5
> 5:1
[1] 5 4 3 2 1

seq関数を用いれば、細かく設定できます。

R Console

> seq(1, 5) # seq(始点, 終点)で始点から終点まで1ずつ増える整数を生成。
[1] 1 2 3 4 5
> seq(1, 5, by=2) # オプションbyにより増減の幅を指定できる。 
[1] 1 3 5
> seq(100, 0, length=4) # オプションlengthで生成する数値の数を指定できる。
[1] 100.00000  66.66667  33.33333   0.00000
> 2^seq(1,10, by=3) # べき乗と組み合わせて使用できる。
[1]    2   16  128 1024

[1] Rプログラミングの小ネタ – Rで繰り返しを含む数列の生成（rep関数、seq関数）

[2] TAKENAKA’s Web Page – おまけ：さまざまなデータ列の生成

乱数を生成する

Rでは様々な確率分布に従った乱数を生成できます[1][2]。

まずは、正規分布を例に説明します。正規分布に従った乱数を生成するにはrnorm関数を使います。

rnorm(生成する乱数の数）

で指定します。生成する乱数の数以外に指定しないと、平均が0、標準偏差が1の標準正規分布に従った乱数が生成されます。

rnorm(生成する乱数の数, 平均値, 標準偏差)

で細かく正規分布の形を指定できます。ここでは、100点満点のテストを仮定して、平均点50点、標準偏差15点に設定して、生成する乱数の数を漸増的に増やしてヒストグラムを書いて見ます。

R Console

> hist(rnorm(10, 50, 15), breaks=20, xlim=c(0,100))

> hist(rnorm(50, 50, 15), breaks=20, xlim=c(0,100))

> hist(rnorm(100, 50, 15), breaks=20, xlim=c(0,100))

> hist(rnorm(1000, 50, 15), breaks=20, xlim=c(0,100))

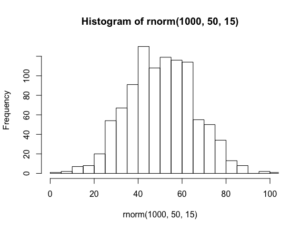
相当なサンプル数でないと正規分布に従うようなヒストグラムにならないことが確認できます。

確率分布に従わない一様乱数を生成するにはrunif関数を使います。整数が必要な場合にはas.integer関数と合わせて使うと便利です。

R Console

> runif(20, min = 1, max = 100) # 一様乱数を20個生成。オプションminとmaxで範囲を指定。
 [1] 37.830902 27.355288 57.816045 67.620597 66.734761 85.002115 79.612580 54.935104
 [9] 79.061071 96.390732  6.012057 71.292323 10.219624 18.756812 81.505803 61.341435
[17] 20.867242 28.862326 67.673707 70.296981
> as.integer(runif(20, min = 1, max = 100)) # as.integerと組み合わせて整数を生成。
 [1] 77 19 55  2 21 71 14 22 93 46 95 20 85 78 10 83 44 24  8 52

[1] R-Tips – 60. 確率分布と乱数

[2] Jin’s HP – Rと確率分布

乱数生成の実用例

t検定のためのサンプルデータ生成

60人クラスのテストの点数を想定しています。

R Console

> size <- 60 # 対象者数
> x1 <- rnorm(n=size, mean=60, sd=10) # n=sizeの部分は直接数値を入れても良い。
> x2 <- rnorm(n=size, mean=60, sd=10) 
> t.test(x1, x2,var.equal = TRUE , paired=FALSE)$p.value # $p.valueを付けてp値のみを表示。
[1] 0.3056895

> size <- 60 
> x1 <- rnorm(n=size, mean=60, sd=10) 
> x2 <- rnorm(n=size, mean=55, sd=10) # 2つの集団の平均値を5ずらす。
> t.test(x1, x2,var.equal = TRUE , paired=FALSE)$p.value
[1] 0.02313767

相関関係を持つサンプルデータ生成

参考資料[1]

R Console

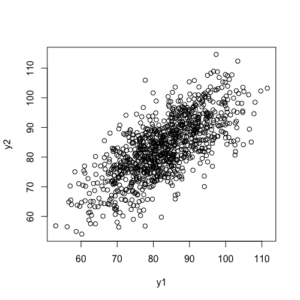
> rho <- 0.7 # 想定する相関係数。 
> n <- 1000
> x <- rnorm(n=n, mean=60, sd=10) 
> e1 <- rnorm(n=n, mean=60, sd=10) 
> e2 <- rnorm(n=n, mean=60, sd=10) 
> y1 <- sqrt(rho)*x+sqrt(1-rho)*e1 
> y2 <- sqrt(rho)*x+sqrt(1-rho)*e2 
> cor(y1, y2) # 生成したy1とy2の相関係数。
[1] 0.7120993
> plot(y1, y2)

等分散性検定のためのサンプルデータ生成

rnormのオプションsdを変更して、等分散性のシミュレーションを行って見ます。

R Console

> a <- rnorm(n=20, mean=60, sd=10) # 平均60、標準偏差10の乱数を20個生成。 
> b <- rnorm(n=20, mean=60, sd=5) # 平均60、標準偏差5の乱数を20個生成。
> ab <- c(a,b) # ベクトルaとbを1つのベクトルに合成。 
> c <- factor(rep(c(1,2), each=20)) # ベクトルcにaとbを群分類するためのfactor型ベクトルを生成。
> library(car) # パッケージcarに含まれるLeveneTestを使い、等分散性を検定。
> leveneTest(ab,c)
Levene's Test for Homogeneity of Variance (center = median)
      Df F value   Pr(>F)   
group  1  7.4934 0.009368 ** # 棄却され、等分散ではないことが示された。
      38                    
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

> a <- rnorm(n=20, mean=60, sd=7) # 今度はsdを7と5に設定。
> b <- rnorm(n=20, mean=60, sd=5) 
> ab <- c(a,b) 
> c <- factor(rep(c(1,2), each=20)) 
> library(car)
> leveneTest(ab,c)
Levene's Test for Homogeneity of Variance (center = median)
      Df F value Pr(>F)
group  1  1.1138 0.2979 # 等分散であることが示された。
      38

同じ乱数を生成

set.seedを使って同じ関数を生成できます。

set.seed(任意の整数)

で指定します。

R Console

> rnorm(5) # 正規分布に従った乱数を先生。
[1]  0.7383247  0.5757814 -0.3053884  1.5117812  0.3898432
> rnorm(5) # 毎回異なる数値が生成される。
[1] -0.62124058 -2.21469989  1.12493092 -0.04493361 -0.01619026
> set.seed(1); rnorm(x) # set.seed()でを使って乱数を生成。
[1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078 -0.8204684  0.4874291
> set.seed(1); rnorm(x) # 上段と同じ数値が生成された。
[1] -0.6264538  0.1836433 -0.8356286  1.5952808  0.3295078 -0.8204684  0.4874291

[1] Makoto Hirakawa, 特任助教 at 広島大学大学院教育学研究科 | SlideShare – Rで架空データの発生