生存時間分析

データの準備：

survivalというパッケージに入っているkidneyというデータを使います。

R Console

> library(survival) # パッケージsurvivalを読み込みます
> head(kidney) # kidneyデータの先頭部分を表示
  id time status age sex disease frail
1  1    8      1  28   1   Other   2.3
2  1   16      1  28   1   Other   2.3
3  2   23      1  48   2      GN   1.9
4  2   13      0  48   2      GN   1.9
5  3   22      1  32   1   Other   1.2
6  3   28      1  32   1   Other   1.2

このデータは、ポータブル腎臓透析カテーテルを用いる際の感染発生までの時間を調べたものです。

time：イベント発生までの時間

status：イベント発生（1：感染発生、0：感染以外でカテーテル抜去）

age：年齢

sex：性別（1：男性、2：女性）

disease：GN：糸球体腎炎、AN：何の略か不明、PKD：多発性嚢胞腎、other：その他

frail：フレイルの推定

R Console

Kaplan-Meier法によるイベント発生までの時間の推定

生存時間分析は、一定期間、継続して観察を行うので、ターゲットとするイベントが生じる以外にも、何らかの要因で観察を打ち切らないといけない状況が出てきます。まず、パッケージsurvivalの中にあるSurvという関数で打ち切りを設定します。

> kidney.Surv <- Surv(kidney$time,kidney$status) # パッケージsurvivalの中にあるSurvという関数を使い、打ち切り情報を付加
> kidney.Surv # 数値は感染発生までの時間を示し、+が付加されている数値は感染以外の理由でで打ち切り
 [1]   8   16   23   13+  22   28  447  318   30   12   24  245    7    9  511   30 
[17]  53  196   15  154    7  333  141    8+  96   38  149+  70+ 536   25+  17    4+
[33] 185  177  292  114   22+ 159+  15  108+ 152  562  402   24+  13   66   39   46+
[49]  12   40  113+ 201  132  156   34   30    2   25  130   26   27   58    5+  43 
[65] 152   30  190    5+ 119    8   54+  16+   6+  78   63    8+
> fit.disease <- survfit(Surv(time, status) ~ disease, data=kidney) # Kaplan-Meier法により疾患で層別化された感染までの時間を算出
> fit.disease
Call: survfit(formula = kidney.Surv ~ kidney$disease) # 疾患別の例数、イベント発生数、感染までの時間（中央値、95%CI）

                      n events median 0.95LCL 0.95UCL
kidney$disease=Other 26     20    141      30     318
kidney$disease=GN    18     14     30      25      NA
kidney$disease=AN    24     18     48      38      NA
kidney$disease=PKD    8      6    115      63      NA

疾患別と同じように、性別で層別化された感染までの時間を算出してみます。

R Console

> fit.sex <- survfit(Surv(time, status) ~ sex, data=kidney) # Kaplan-Meier法により性別で層別化された感染までの時間を算出
> fit.sex
Call: survfit(formula = kidney.Surv ~ kidney$sex) # 性別ごとの例数、イベント発生数、感染までの時間（中央値、95%CI）

              n events median 0.95LCL 0.95UCL
kidney$sex=1 20     18     22      12      63
kidney$sex=2 56     40    130      66     190

Kaplan-Meier曲線の描画

上で作成した疾患により層別化されたデータを元に、Kaplan-Meier曲線を描画してみます。

R Console

> plot(fit.disease, main="Kaplan-Meier estimate", xlab="time", ylab="survival function", col=c("red", "blue", "green","pink"))
> legend("topright", legend=levels(kidney$disease), col=c("red","blue","green","pink"), lty=1)

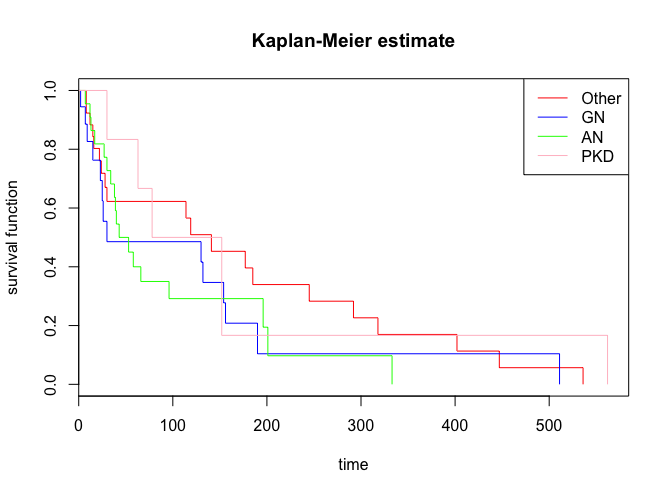
同様に、性別により層別化されたデータを元に、Kaplan-Meier曲線を描画してみます。

R Console

> plot(fit.sex, main="Kaplan-Meier estimate", xlab="time", ylab="survival function", col=c("blue", "red"))
> legend("topright", legend=c("male","female"), col=c("blue","red"), lty=1)

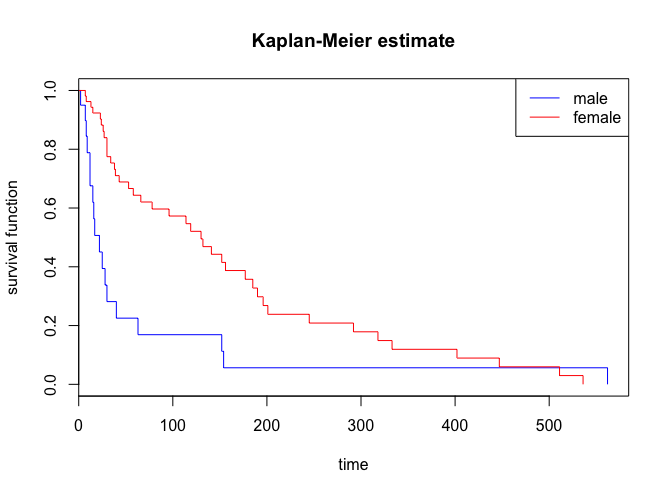
ちなみに、plotのオプションで、conf.int=TRUEを加えると95％信頼区間を描画できます。

R Console

> plot(fit.sex, main="Kaplan-Meier estimate", xlab="time", ylab="survival function", col=c("blue", "red"), conf.int=TRUE)

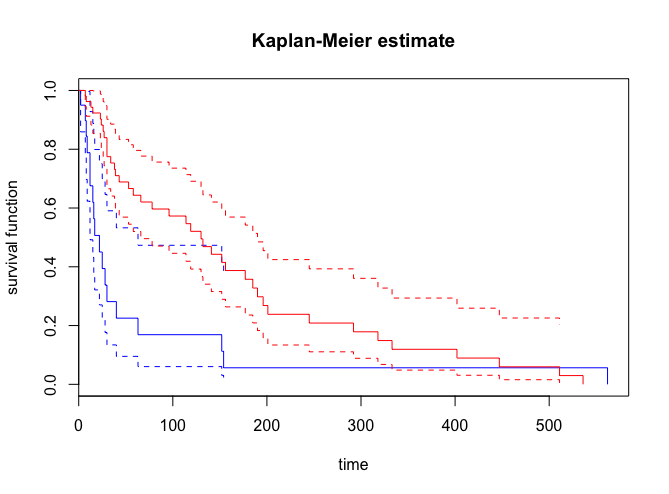
Log-rank検定

Log-rank検定は、層化されたKaplan-Meier曲線に差があるかどうかを調べる検定です。性別で層別化したKaplan-Meier曲線の差を検定してみます。[1]

R Console

> survdiff(Surv(time, status)~sex, data=kidney) # パッケージsurvivalの中のsurvdiff関数を使います。
Call:
survdiff(formula = Surv(time, status) ~ sex, data = kidney)

       N Observed Expected (O-E)^2/E (O-E)^2/V
sex=1 20       18     10.2      5.99      8.31
sex=2 56       40     47.8      1.28      8.31

 Chisq= 8.3  on 1 degrees of freedom, p= 0.004

次に疾患で層別化したKaplan-Meier曲線の差を検定してみます。

R Console

> survdiff(Surv(time, status)~disease, data=kidney)
Call:
survdiff(formula = Surv(time, status) ~ disease, data = kidney)

               N Observed Expected (O-E)^2/E (O-E)^2/V
disease=Other 26       20    23.20     0.442     0.779
disease=GN    18       14    11.62     0.488     0.631
disease=AN    24       18    14.70     0.740     1.070
disease=PKD    8        6     8.48     0.724     0.989

 Chisq= 2.7  on 3 degrees of freedom, p= 0.4

Lon-rank検定では疾患でのイベント発生に差は認められません。

[1] 比例ハザードモデルはとってもtricky！

Cox比例ハザード回帰分析

Cox比例ハザード回帰分析は、共変量を考慮して生存曲線を比較する方法で、多変量解析のひとつです。時間を考慮したロジスティック回帰分析のようなものですね。ハザードというのはアウトカムが発生するリスクという意味で、比例ハザードは、そのリスクが時間の経過によらず一定ということだそうです。リスクが時間の経過によらず一定かどうかを簡単に見分ける方法として2つのKapran-Meier曲線が交差していたら、比例ハザードが成立しないと予想されるそうです [1]。

パッケージsurvivalの中にあるcoxph関数によりCox比例ハザードモデルのパラメータを推定できます。コックス比例ハザードモデルのパラメータの推定方法としては、直接法、Breslowの近似法、Efronの近似法などがあるそうです。coxph関数では、何も指定しないとEfronの近似法が用いられるようですが、method=””でefron、breslow、exactが指定でき、exactで直接法も指定できます [2]。

R Console

> kidney.cox <- coxph(Surv(time, status)~sex+disease, data = kidney) # sex+diseaseで説明変数に性別と疾患を指定
> summary(kidney.cox) # exp(coef)がハザード比ですね
Call:
coxph(formula = Surv(time, status) ~ sex + disease, data = kidney)

  n= 76, number of events= 58 

              coef exp(coef) se(coef)      z Pr(>|z|)    
sex        -1.4774    0.2282   0.3569 -4.140 3.48e-05 ***
diseaseGN   0.1392    1.1494   0.3635  0.383   0.7017    
diseaseAN   0.4132    1.5116   0.3360  1.230   0.2188    
diseasePKD -1.3671    0.2549   0.5889 -2.321   0.0203 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

           exp(coef) exp(-coef) lower .95 upper .95
sex           0.2282     4.3815   0.11339    0.4594
diseaseGN     1.1494     0.8700   0.56368    2.3437
diseaseAN     1.5116     0.6616   0.78245    2.9202
diseasePKD    0.2549     3.9238   0.08035    0.8084

Concordance= 0.696  (se = 0.039 )
Rsquare= 0.206   (max possible= 0.993 )
Likelihood ratio test= 17.56  on 4 df,   p=0.002
Wald test            = 19.77  on 4 df,   p=6e-04
Score (logrank) test = 19.97  on 4 df,   p=5e-04

method=”exact”を指定して直接法で計算してみます。

R Console

> kidney.cox.exact <- coxph(Surv(time, status)~sex+disease, method = "exact", data = kidney) 
> summary(kidney.cox.exact)
Call:
coxph(formula = Surv(time, status) ~ sex + disease, data = kidney, 
    method = "exact")

  n= 76, number of events= 58 

              coef exp(coef) se(coef)      z Pr(>|z|)    
sex        -1.4972    0.2238   0.3627 -4.128 3.65e-05 ***
diseaseGN   0.1462    1.1574   0.3655  0.400   0.6891    
diseaseAN   0.4257    1.5306   0.3381  1.259   0.2080    
diseasePKD -1.3877    0.2496   0.5924 -2.343   0.0191 *  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

           exp(coef) exp(-coef) lower .95 upper .95
sex           0.2238     4.4692   0.10992    0.4555
diseaseGN     1.1574     0.8640   0.56546    2.3691
diseaseAN     1.5306     0.6533   0.78900    2.9693
diseasePKD    0.2496     4.0057   0.07818    0.7972

Concordance= 0.696  (se = 0.039 )
Rsquare= 0.208   (max possible= 0.992 )
Likelihood ratio test= 17.73  on 4 df,   p=0.001
Wald test            = 19.64  on 4 df,   p=6e-04
Score (logrank) test = 19.92  on 4 df,   p=5e-04

何も指定しないEfronの近似法より、method=”exact”と指定した方がハザード比が若干有意になっています。

coxph関数では、尤度比の検定（Likelihood ratio test）、ワルド検定（Wald test）、スコア検定（Score (logrank) test）が行われており、これらは説明変数が正規分布に従うことを仮定した検定になっています [2]。

coxphにより作られたモデルを当てはめて生存時間を推定するには、survfit関数を使います。

R Console

> kidney.cox.fit <- survfit(kidney.cox) 
> summary(kidney.cox.fit)
Call: survfit(formula = kidney.cox)

 time n.risk n.event survival std.err lower 95% CI upper 95% CI
    2     76       1  0.99018 0.00985     0.971059        1.000
    7     71       2  0.96856 0.01831     0.933335        1.000
    8     69       2  0.94641 0.02422     0.900102        0.995
    9     65       1  0.93499 0.02685     0.883820        0.989
   12     64       2  0.91106 0.03177     0.850869        0.976
   13     62       1  0.89844 0.03411     0.834007        0.968
   15     60       2  0.87273 0.03844     0.800550        0.951
   16     58       1  0.85959 0.04046     0.783848        0.943
   17     56       1  0.84591 0.04246     0.766654        0.933
   22     55       1  0.83144 0.04446     0.748706        0.923
   23     53       1  0.81625 0.04646     0.730084        0.913
   24     52       1  0.80113 0.04830     0.711843        0.902
   25     50       1  0.78592 0.05004     0.693710        0.890
   26     48       1  0.76976 0.05184     0.674573        0.878
   27     47       1  0.75369 0.05350     0.655802        0.866
   28     46       1  0.73761 0.05503     0.637273        0.854
   30     45       4  0.67000 0.06032     0.561621        0.799
   34     41       1  0.65287 0.06137     0.543011        0.785
   38     40       1  0.63574 0.06232     0.524602        0.770
   39     39       1  0.61861 0.06317     0.506390        0.756
   40     38       1  0.60147 0.06392     0.488373        0.741
   43     37       1  0.58250 0.06463     0.468646        0.724
   53     35       1  0.56288 0.06531     0.448382        0.707
   58     33       1  0.54279 0.06594     0.427786        0.689
   63     32       1  0.52270 0.06642     0.407467        0.671
   66     31       1  0.50281 0.06677     0.387591        0.652
   78     29       1  0.48209 0.06708     0.367010        0.633
   96     28       1  0.46208 0.06717     0.347515        0.614
  114     25       1  0.44051 0.06735     0.326443        0.594
  119     24       1  0.41929 0.06734     0.306055        0.574
  130     23       1  0.39842 0.06715     0.286338        0.554
  132     22       1  0.37781 0.06678     0.267181        0.534
  141     21       1  0.35745 0.06624     0.248591        0.514
  152     19       2  0.31584 0.06486     0.211190        0.472
  154     17       1  0.29608 0.06387     0.194001        0.452
  156     16       1  0.27265 0.06289     0.173487        0.429
  177     14       1  0.24811 0.06174     0.152353        0.404
  185     13       1  0.22436 0.06018     0.132633        0.380
  190     12       1  0.20143 0.05822     0.114311        0.355
  196     11       1  0.17910 0.05588     0.097163        0.330
  201     10       1  0.15675 0.05322     0.080583        0.305
  245      9       1  0.13440 0.05018     0.064649        0.279
  292      8       1  0.11323 0.04664     0.050506        0.254
  318      7       1  0.09332 0.04259     0.038149        0.228
  333      6       1  0.07474 0.03804     0.027567        0.203
  402      5       1  0.05617 0.03300     0.017760        0.178
  447      4       1  0.03948 0.02728     0.010191        0.153
  511      3       1  0.02491 0.02093     0.004800        0.129
  536      2       1  0.01224 0.01383     0.001336        0.112
  562      1       1  0.00318 0.00613     0.000073        0.139

survfit関数で推定された生存曲線および信頼区間のグラフを描画してみます。

R Console

> plot(kidney.cox.fit, main="Cox proportional hazard model", xlab="time", ylab="survival probability")

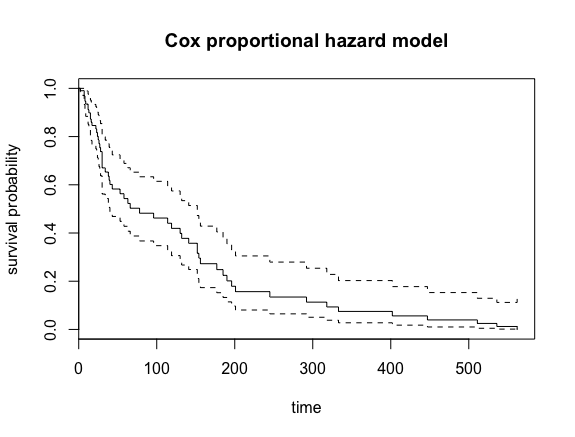
[1] EM Alliance – 第７回EMA-JC　解説　カプランマイヤー生存曲線

[2] mitsurukikkawa – 生存時間分析(survival analysis)

Cox比例ハザード回帰分析のモデル信頼性の確認

残差分析

生存時間分析の残渣分析には、マルチンゲール残差(martingale residuals)、シェーンフィールド残差(Schoenfeld residuals)、スコア残差(score residuals)、デヴィアンス残差(deviance residuals)などいくつかの方法があります [1]。Cox比例ハザード回帰分析の残差分析はresiduals関数を用います。デフォルトでは、マルチンゲール残差が適用されますが、他の方法を指定することもできます。ここでは、デヴィアン残差のプロットも描画してみます。

ちなみに、残差分析そのものについては、このあたりが参考になりました [2]。

R Console

> scatter.smooth(residuals(kidney.cox)) # scatter.smoothは散布図を描き、Lowess平滑化 [3] による平滑化曲線を描く関数 
>abline(h=0,lty=3,col=2)

R Console

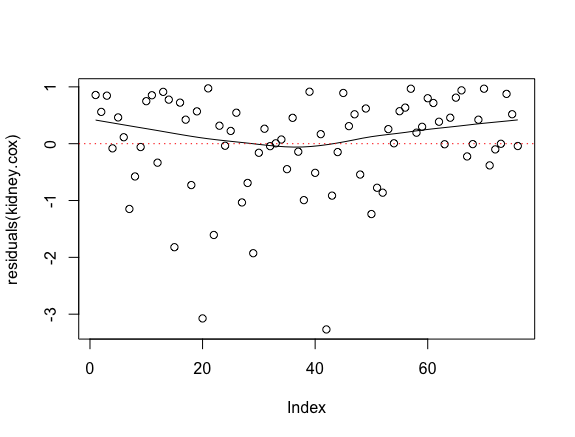
> scatter.smooth(residuals(kidney.cox, type="deviance"))
> abline(h=0,lty=3,col=2)

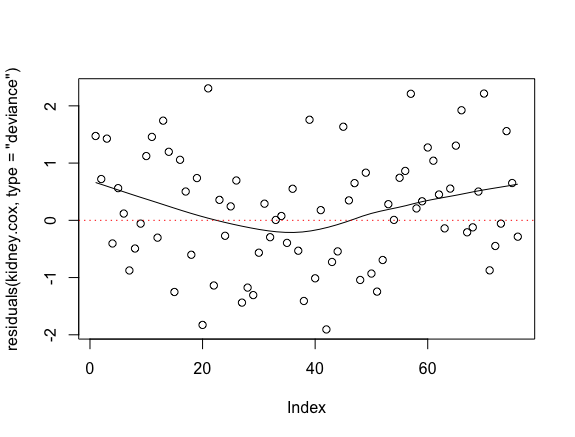
ハザードの比例性の分析

Cox比例ハザード回帰分析は、リスクが時間の経過によらず一定という前提に基づいて行われているそうです。パッケージsurvivalには、cox.zphという比例性を分析する関数があります。

R Console

> kidney.zph<-cox.zph(kidney.cox) > kidney.zph
                rho   chisq     p
sex         0.18839 2.60676 0.106
diseaseGN  -0.01392 0.01123 0.916
diseaseAN   0.06162 0.20036 0.654
diseasePKD  0.00701 0.00438 0.947
GLOBAL           NA 4.20781 0.379

cox.zphで仮説が棄却されると比例ハザードの仮定が充たされていない可能性があります。今回は、すべてp>0.05なので棄却されず、比例ハザード性があると言えます。

cox.zph関数で得られた情報をplotで描画すると、シェーンフィールド残差プロットに、スプライン平滑化された曲線と標準誤差の2倍の信頼区間が示されるグラフを作成することができます。

R Console

> par(mfrow=c(1,4)) # 1列4行のレイアウトでグラフを並べる指示
> plot(kidney.zph)

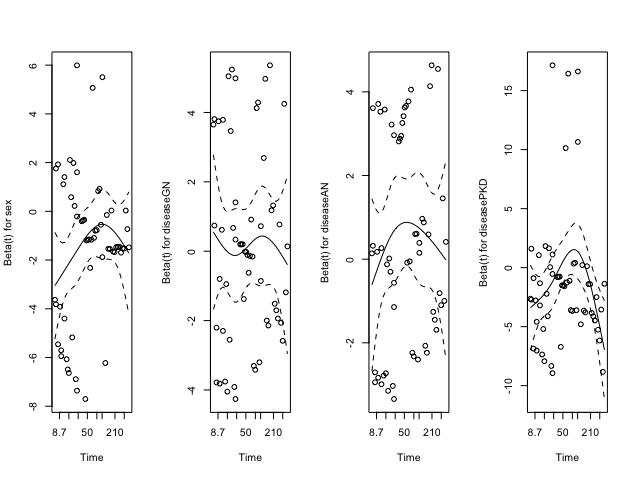
時間経過に伴うβの変化をみます。PKDが終盤にかけて意味ありげに下降していますが、許容範囲内なのでしょうか。よく分かりません。

交互作用を考慮したCox比例ハザード回帰分析

重回帰分析のように、Cox比例ハザード回帰分析でも説明変数の交互作用効果を取り入れたモデルを作ることができます。

R Console

> kidney.cox2 <- coxph(Surv(time, status) ~ (sex+disease+age)^2, data = kidney) # ^2によりそれぞれの交互作用を取り入れる 
> summary(kidney.cox2)
Call:
coxph(formula = Surv(time, status) ~ (sex + disease + age)^2, 
    data = kidney)

  n= 76, number of events= 58 

                     coef  exp(coef)   se(coef)      z Pr(>|z|)  
sex            -2.613e+00  7.330e-02  1.210e+00 -2.159   0.0308 *
diseaseGN      -7.846e-01  4.563e-01  3.041e+00 -0.258   0.7964  
diseaseAN      -1.883e+00  1.522e-01  2.581e+00 -0.729   0.4658  
diseasePKD     -1.437e+01  5.761e-07  5.595e+00 -2.568   0.0102 *
age             2.107e-02  1.021e+00  7.526e-02  0.280   0.7795  
sex:diseaseGN   9.954e-01  2.706e+00  1.343e+00  0.741   0.4586  
sex:diseaseAN   1.301e+00  3.672e+00  1.223e+00  1.063   0.2876  
sex:diseasePKD  3.710e+00  4.084e+01  1.691e+00  2.193   0.0283 *
sex:age        -4.400e-03  9.956e-01  4.045e-02 -0.109   0.9134  
diseaseGN:age  -2.313e-02  9.771e-01  2.879e-02 -0.803   0.4217  
diseaseAN:age  -3.377e-03  9.966e-01  2.995e-02 -0.113   0.9102  
diseasePKD:age  1.396e-01  1.150e+00  1.114e-01  1.253   0.2103  
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

               exp(coef) exp(-coef) lower .95 upper .95
sex            7.330e-02  1.364e+01 6.838e-03 7.858e-01
diseaseGN      4.563e-01  2.192e+00 1.177e-03 1.769e+02
diseaseAN      1.522e-01  6.571e+00 9.671e-04 2.395e+01
diseasePKD     5.761e-07  1.736e+06 9.958e-12 3.332e-02
age            1.021e+00  9.792e-01 8.812e-01 1.184e+00
sex:diseaseGN  2.706e+00  3.696e-01 1.946e-01 3.762e+01
sex:diseaseAN  3.672e+00  2.723e-01 3.340e-01 4.038e+01
sex:diseasePKD 4.084e+01  2.448e-02 1.484e+00 1.124e+03
sex:age        9.956e-01  1.004e+00 9.197e-01 1.078e+00
diseaseGN:age  9.771e-01  1.023e+00 9.235e-01 1.034e+00
diseaseAN:age  9.966e-01  1.003e+00 9.398e-01 1.057e+00
diseasePKD:age 1.150e+00  8.697e-01 9.242e-01 1.431e+00

Concordance= 0.712  (se = 0.041 )
Rsquare= 0.351   (max possible= 0.993 )
Likelihood ratio test= 32.86  on 12 df,   p=0.001
Wald test            = 34.17  on 12 df,   p=6e-04
Score (logrank) test = 44.45  on 12 df,   p=1e-05

> library(MASS) # パッケージMASSの読み込み
> stepAIC(kidney.cox2) # 交互作用も取り入れたモデルの説明変数をStepwise法にて絞り込み
Start:  AIC=366.95
Surv(time, status) ~ (sex + disease + age)^2

              Df    AIC
- disease:age  3 362.99
- sex:age      1 364.96
           366.95
- sex:disease  3 367.26

Step:  AIC=362.99
Surv(time, status) ~ sex + disease + age + sex:disease + sex:age

              Df    AIC
- sex:age      1 361.36
           362.99
- sex:disease  3 368.67

Step:  AIC=361.36
Surv(time, status) ~ sex + disease + age + sex:disease

              Df    AIC
- age          1 359.54
           361.36
- sex:disease  3 368.16

Step:  AIC=359.54
Surv(time, status) ~ sex + disease + sex:disease

              Df    AIC
           359.54
- sex:disease  3 366.24
Call:
coxph(formula = Surv(time, status) ~ sex + disease + sex:disease, 
    data = kidney)

                     coef  exp(coef)   se(coef)      z        p
sex            -2.5252779  0.0800361  0.5659622 -4.462 8.12e-06
diseaseGN      -1.3415792  0.2614325  1.3037724 -1.029 0.303481
diseaseAN      -1.4180768  0.2421793  1.4840553 -0.956 0.339304
diseasePKD     -7.3819153  0.0006224  1.9493785 -3.787 0.000153
sex:diseaseGN   0.8312922  2.2962840  0.7604435  1.093 0.274320
sex:diseaseAN   1.0754002  2.9311656  0.8156353  1.318 0.187342
sex:diseasePKD  4.2144726 67.6584758  1.1501090  3.664 0.000248

Likelihood ratio test=30.26  on 7 df, p=8.496e-05
n= 76, number of events= 58

ステップワイズ法の結果を見ると、性別とPKD（多発性嚢胞腎）の間に交互作用があり、モデルの有意な説明因子になっていることが分かります。

最後に、交互作用がどうなっているのか性別と疾患で層別化した分析を行って、確認してみます。

R Console

> survfit(Surv(time,status) ~sex+disease, data=kidney)
Call: survfit(formula = Surv(time, status) ~ sex + disease, data = kidney)

                      n events median 0.95LCL 0.95UCL
sex=1, disease=Other  6      6     19      12      NA
sex=1, disease=GN     6      6     12       7      NA
sex=1, disease=AN     4      3     17      12      NA
sex=1, disease=PKD    4      3    152      63      NA
sex=2, disease=Other 20     14    185     119      NA
sex=2, disease=GN    12      8    132      30      NA
sex=2, disease=AN    20     15     58      39      NA
sex=2, disease=PKD    4      3     78      30      NA

多発性嚢胞腎の場合、男性より女性の方が倍近く早く感染症を起こしやすいことが確認できます。交互作用の確認は大切なんですね。

[1] mitsurukikkawa – 生存時間分析(survival analysis)

[2] 統計WEB – 27-3. 予測値と残差

[3] MathWorks – Lowess 平滑化