二項ロジスティック回帰分析

データの読み込みと準備

Rに元から入っているTitanicデータセットを使います。Titanicデータはtable型なので、data.frame型に変更します。さらに、同じ属性の人がFreq列に人数としてまとめられているので、これを展開します。

R Console

> Titanic # Titanicデータを表示。
, , Age = Child, Survived = No

      Sex
Class  Male Female
  1st     0      0
  2nd     0      0
  3rd    35     17
  Crew    0      0

, , Age = Adult, Survived = No

      Sex
Class  Male Female
  1st   118      4
  2nd   154     13
  3rd   387     89
  Crew  670      3

, , Age = Child, Survived = Yes

      Sex
Class  Male Female
  1st     5      1
  2nd    11     13
  3rd    13     14
  Crew    0      0

, , Age = Adult, Survived = Yes

      Sex
Class  Male Female
  1st    57    140
  2nd    14     80
  3rd    75     76
  Crew  192     20

> class(Titanic) # Titanicデータのclass分類での型を調べる。table型である。
[1] "table"
> x <- data.frame(Titanic) # データフレームに変更。 
> head(x) # データxの先頭から数行を表示。Freqに35と記載されているが、これはこの属性の人が35人いるということ。
  Class    Sex   Age Survived Freq
1   1st   Male Child       No    0
2   2nd   Male Child       No    0
3   3rd   Male Child       No   35
4  Crew   Male Child       No    0
5   1st Female Child       No    0
6   2nd Female Child       No    0
> str(x) # ついでにデータxの型を調べる。Freq以外はFactor型。
'data.frame':	32 obs. of  5 variables:
 $ Class   : Factor w/ 4 levels "1st","2nd","3rd",..: 1 2 3 4 1 2 3 4 1 2 ...
 $ Sex     : Factor w/ 2 levels "Male","Female": 1 1 1 1 2 2 2 2 1 1 ...
 $ Age     : Factor w/ 2 levels "Child","Adult": 1 1 1 1 1 1 1 1 2 2 ...
 $ Survived: Factor w/ 2 levels "No","Yes": 1 1 1 1 1 1 1 1 1 1 ...
 $ Freq    : num  0 0 35 0 0 0 17 0 118 154 ...
> y <- data.frame( Class=rep(x$Class, x$Freq), Sex=rep(x$Sex, x$Freq), Age=rep(x$Age, x$Freq), Survived=rep(x$Survived, x$Freq)) # rep関数はrep(x,y)でxをy個繰り返すというように記述する。Freuに記載されている数だけその行の要素を繰り返すベクトルを作成し、data.frame型にまとめ、yに指定。 
> head(y) # yの先頭数行を表示。xでFreqが35の要素が展開されているのが確認できる。
  Class  Sex   Age Survived
1   3rd Male Child       No
2   3rd Male Child       No
3   3rd Male Child       No
4   3rd Male Child       No
5   3rd Male Child       No
6   3rd Male Child       No

二項ロジスティック回帰分析を実行

R Console

> glmy <- glm(Survived ~ Class+Sex+Age, data=y, family ="binomial") 
> summary(glmy)

Call:
glm(formula = Survived ~ Class + Sex + Age, family = "binomial", 
    data = y)

Deviance Residuals: 
    Min       1Q   Median       3Q      Max  
-2.0812  -0.7149  -0.6656   0.6858   2.1278  

Coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)   0.6853     0.2730   2.510   0.0121 *  
Class2nd     -1.0181     0.1960  -5.194 2.05e-07 ***
Class3rd     -1.7778     0.1716 -10.362  < 2e-16 ***
ClassCrew    -0.8577     0.1573  -5.451 5.00e-08 ***
SexFemale     2.4201     0.1404  17.236  < 2e-16 ***
AgeAdult     -1.0615     0.2440  -4.350 1.36e-05 ***
---
Signif. codes:  0 ‘***’ 0.001 ‘**’ 0.01 ‘*’ 0.05 ‘.’ 0.1 ‘ ’ 1

(Dispersion parameter for binomial family taken to be 1)

    Null deviance: 2769.5  on 2200  degrees of freedom
Residual deviance: 2210.1  on 2195  degrees of freedom
AIC: 2222.1

Number of Fisher Scoring iterations: 4

CoefficientsのEstimateに説明変数の回帰係数が計算されています。Std.Errorに回帰係数の標準誤差も計算されています。ただ、これではオッズ比が分かりません。回帰係数の対数を計算すればオッズ比になるのですが、面倒なので、パッケージepiDisplayの中にあるlogistic.display関数を使うと簡単に計算できます。

R Console

> logistic.display(glmy)

Logistic regression predicting Survived : Yes vs No 
 
                    crude OR(95%CI)     adj. OR(95%CI)      P(Wald's test) P(LR-test)
Class: ref.=1st                                                            < 0.001   
   2nd              0.42 (0.31,0.59)    0.36 (0.25,0.53)    < 0.001                  
   3rd              0.2 (0.15,0.27)     0.17 (0.12,0.24)    < 0.001                  
   Crew             0.19 (0.14,0.25)    0.42 (0.31,0.58)    < 0.001                  
                                                                                     
Sex: Female vs Male 10.15 (8.03,12.83)  11.25 (8.54,14.81)  < 0.001        < 0.001   
                                                                                     
Age: Adult vs Child 0.41 (0.28,0.61)    0.35 (0.21,0.56)    < 0.001        < 0.001 Log-likelihood = -1105.0306 No. of observations = 2201 AIC value = 2222.0611 
> logistic.display(glmy, simplified=TRUE) # simplified=TRUEのオプションを付けると成形されたオッズ比、95%信頼区間、p値が算出されます。
 
                  OR lower95ci  upper95ci     Pr(>|Z|)
Class2nd   0.3612825 0.2460447  0.5304933 2.053331e-07
Class3rd   0.1690159 0.1207510  0.2365727 3.691891e-25
ClassCrew  0.4241466 0.3115940  0.5773549 5.004592e-08
SexFemale 11.2465380 8.5408719 14.8093331 1.431830e-66
AgeAdult   0.3459219 0.2144193  0.5580746 1.360490e-05

ロジスティック回帰分析の評価

Hosmer-Lemeshow検定

適合度の検定はAICの他にHosmer-Lemeshow検定も行われます。これはパッケージResourceSelectionにあるhoslem.test関数で実行できます[3]。hoslem.test(実測値, 傾向スコア)と指定します。

R Console

> library(ResourceSelection)
> hoslem.test(glmy$y, glmy$fitted.values)

	Hosmer and Lemeshow goodness of fit (GOF) test

data:  glmy$y, fitted(glmy)
X-squared = 16.733, df = 8, p-value = 0.03301

一般的にHosmer-Lemeshow検定ではp値が0.05より大きければ適合しているとみなすようですが[1]、今回は0.03なので適合度は良くないのかもしれません。

擬似R²

ロジスティック回帰分析において決定係数を求めることができないようですが、擬似的にR²を計算することができます。パッケージBaylorEdPsychにあるPseudoR2関数を使います。

R Console

> library(BaylorEdPsych)
> PseudoR2(glmy)
        McFadden     Adj.McFadden        Cox.Snell       Nagelkerke McKelvey.Zavoina 
       0.2019875        0.1969324        0.2244286        0.3135111        0.3016679 
          Effron            Count        Adj.Count              AIC    Corrected.AIC 
       0.2587763        0.7782826        0.3136428     2222.0611057     2222.0993919

[1] ill-identified diary – [離散選択] ロジットモデルの決定係数 – ill-identified diary

多重共線性

共通の性質を持つ説明変数が存在すると回帰式が不安定になることがあり、これを多重共線性というそうですが、重回帰分析と同様にVIFを計算することもあれば[1]、ロジスティック回帰分析ではVIFは不適合とされることもあるようです[2]。VIFの計算方法は、このブログの重回帰分析（全ての変数を強制投入）モデル式の多重共線性を確認を参照ください。

[1] 天理医学紀要 – ロジスティック回帰分析と傾向スコア (propensity score) 解析（大林準）

[2] 薬剤師のためのEBMお悩み相談所－基礎から実践まで – ロジスティック回帰分析における多重共線性の評価に関して

[3] The Stats Geek – The Hosmer-Lemeshow goodness of fit test for logistic regression

ROC解析による評価

実測値（今回は実際に生存したか死亡したか）と二項ロジスティック回帰分析で得られる予測値との関係からROC解析を行い、ロジスティック回帰モデルを評価します[1]。

ROC解析

パッケージpROCを使います。roc関数を使って、ROC曲線や種々の数値を計算します。ロジスティック回帰分析から得られたデータを利用し、roc(目的変数, 傾向スコア)と指定します。

R Console

> library(pROC) #パッケージpROCの読み込み
> ROC <- roc(response=glmy$y, predictor=glmy$fitted.values) # roc関数にてROC解析を実行。 
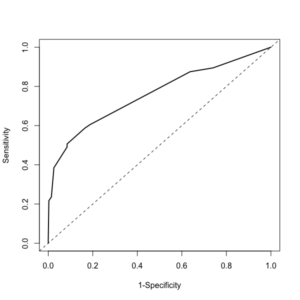
> plot(1-ROC$specificities, ROC$sensitivities, xlab="1-Specificity", ylab="Sensitivity", type="l", lwd=2) # ROC曲線の描画。オプションlwd=数字で線の太さを指定。
> abline(a=0,b=1,lty=2) # 直線の描画。lty=2で破線として指定。

> CI <- ci.auc(ROC, conf.level=0.95) # AUCの信頼区間を計算。ci.aucもパッケージpROCに含まれる関数。 
> cutoff <- coords(ROC, x="best", ret=c("threshold", "sensitivity", "specificity", "ppv", "npv"), best.method="closest.topleft") # coords関数もパッケージpROCに含まれる関数で、ROC曲線の種々の座標を求めることができる。
> c.point <- cutoff[1] # ロジスティック回帰モデルによる予測値のカットオフ値を指定。 
> beta <- coef(glmy) # ロジスティックモデルの回帰係数（対数オッズ比）を指定。
> cutoff.variable <- (log(c.point/(1-c.point))-beta[1])/beta[2] # 元の変数のカットオフ値を計算 
> #ここから結果の表示。
> ROC$auc # ROC曲線の曲線下面積AUC（C統計量とも呼ばれる）
Area under the curve: 0.7597
> CI # 曲線下面積AUCの95%信頼区間
95% CI: 0.7373-0.7821 (DeLong)
> c.point # 回帰分析モデル上のカットオフ値
threshold 
0.2383291
> cutoff.variable # #説明変数が1変数の場合の最適カットオフ値（説明変数が複数ある場合は無視） 
> cutoff[2:5]
#sensitivityは 感度（%表記なら100倍）
#specificityは特異度（%表記なら100倍）
#ppvは陽性的中率（positive predictive value)（%表記なら100倍）
#npvは陰性的中率NPV（negative predictive value）（%表記なら100倍）
sensitivity specificity         ppv         npv 
  0.6047820   0.8127517   0.6064880   0.8116622

[1] 臨床医のためのRコマンダーによる医学統計解析マニュアル – ROC曲線_AUCの差の検定_NRIとIDI-臨床医のためのRコマンダーによる医学統計解析マニュアル

2つのロジスティック回帰モデルを比較評価

ROC解析で計算されたAUC値を用いて、2つのロジスティック回帰モデルを比較評価することができます。AUC値の差を検定します。ここでは、説明変数に性別のみを指定したロジスティック回帰モデルglmy2を比較対象にすることにします。

R Console

# ↓元のロジスティック回帰モデルはこちらです↓
# glmy <- glm(Survived ~ Class+Sex+Age, data=y, family ="binomial") 
# 年齢を除去してglmy2を定義します。 
> glmy2 <- glm(Survived ~ Sex, data=y, family ="binomial")

以下にglmy2のROC解析を行います。

R Console

> library(pROC) # パッケージpROCの読み込み
> ROC2 <- roc(response=glmy2$y, predictor=glmy2$fitted.values) # roc関数にてROC解析を行う。 
> par(new=TRUE) # 先に描いたglmyのROC曲線に追加してROC曲線を描画。
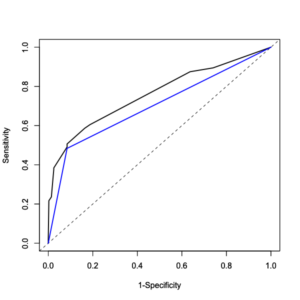
> plot(1-ROC2$specificities, ROC2$sensitivities, xlab="1-Specificity", ylab="Sensitivity", type="l", lwd=2, col="blue") # ROC曲線の描画。オプションlwd=数字で線の太さを指定。オプションcol="blue"で青い線を指定。


> CI2 <- ci.auc(ROC2, conf.level=0.95) # AUCの信頼区間を計算。 
> cutoff2 <- coords(ROC2, x="best", ret=c("threshold", "sensitivity", "specificity", "ppv", "npv"), best.method="closest.topleft") 
> c.point2 <- cutoff2[1] # モデル上のカットオフ値を指定。 
> beta2 <- coef(glmy2) # ロジスティックモデルの回帰係数（対数オッズ比）を指定。
> cutoff.variable <- (log(c.point/(1-c.point))-beta[1])/beta[2] # 目的変数の実測値のカットオフ値を計算。  
> #ここから結果
> ROC2$auc # ROC曲線の曲線下面積AUC（C統計量とも呼ばれる）
Area under the curve: 0.6996
> CI2 # 曲線下面積AUCの95%信頼区間
95% CI: 0.6799-0.7193 (DeLong)
> c.point2 # 回帰分析モデル上のカットオフ値
threshold 
0.4719655 
> cutoff.variable # 説明変数が1変数の場合の最適カットオフ値（説明変数が複数ある場合は無視）
threshold 
 1.814351 
> cutoff2[2:5]
sensitivity specificity         ppv         npv 
  0.4838256   0.9154362   0.7319149   0.7879838

AUCはglmy2の方が低値になりました。

ROCとROC2におけるAUC値の差の比較を以下のように計算します。

R Console

> roc.test(ROC, ROC2, method="delong", alternative="two.sided")

	DeLong's test for two correlated ROC curves

data:  ROC and ROC2
Z = 7.8016, p-value = 6.115e-15
alternative hypothesis: true difference in AUC is not equal to 0
sample estimates:
AUC of roc1 AUC of roc2 
  0.7597259   0.6996309

データの読み込みと準備

二項ロジスティック回帰分析を実行

ロジスティック回帰分析の評価

Hosmer-Lemeshow検定

擬似R2

多重共線性

ROC解析による評価

ROC解析

2つのロジスティック回帰モデルを比較評価

コメントを残す コメントをキャンセル

擬似R²

コメントを残すコメントをキャンセル