二元（多元）配置分散分析

SHARE

Rによる二元配置分散分析についてはこちら[1]のページなどの解説が分かりやすいです。

二元配置分散分析や三元以上の多元配置分散分析、さらにそれぞれの要因が繰り返しのある（対応のある）、繰り返しのない（対応のない）の区別など考慮したりなど、頭の中がこんがらがりそうになります。このような問題を解決するために、私は二元配置分散ん分析にはANOVA君[2]を使うことが多いです。ここではANOVA君を使った分析を紹介します。

[1] Jin’s HP – Rと分散分析

[2] 井関龍太のページ – ANOVA君

ANOVA君のインストール

こちらのページ[1]を参考にインストールします。私はdropboxに入れておいて複数のMacから読み込んでいます。

R Console 

source('~/Dropbox/r/anovakun_482.txt', encoding = 'CP932') # macでは文字コードを指定するために「encoding='CP932'」のオプションを指定します。
[1] 井関龍太のページ  – ANOVA君/ANOVA君の使い方

 

データの読み込み

多元配置分散分析のサンプルデータを提供してくださっているとても便利なページがこちら[1]です。今回は、「1要因に対応がある2要因分散分析(SPFp.qデザイン) データ数が異なる」のデータを使いたいと思います。

このサンプルデータは、a要因とb要因の2要因からなる二元配置分散分析のデータを生成してみます。a要因は2水準の対応のない要因、b要因は4水準で対応のある要因とします。

R Console 
SPFp.q <- data.frame( s = factor(c(rep(1:5, 4), rep(6:9, 4))), a = factor(c(rep(1, 20), rep(2, 16))), b = factor(c(rep(1, 5), rep(2, 5), rep(3, 5), rep(4, 5), rep(1, 4), rep(2, 4), rep(3, 4), rep(4, 4))), result = c(3,3,1,3,5, 4,3,4,5,7, 6,6,6,4,8, 5,7,8,7,9, 3,5,2,4, 2,6,3,6, 3,2,3,6, 2,3,3,4)) 
> SPFp.q # データを確認。sは被験者、aは検者間要因（対応のない要因）、bは検者内要因（対応のある要因）
s a b result
1 1 1 1 3
2 2 1 1 3
3 3 1 1 1
4 4 1 1 3
5 5 1 1 5
6 1 1 2 4
7 2 1 2 3
8 3 1 2 4
9 4 1 2 5
10 5 1 2 7
11 1 1 3 6
12 2 1 3 6
13 3 1 3 6
14 4 1 3 4
15 5 1 3 8
16 1 1 4 5
17 2 1 4 7
18 3 1 4 8
19 4 1 4 7
20 5 1 4 9
21 6 2 1 3
22 7 2 1 5
23 8 2 1 2
24 9 2 1 4
25 6 2 2 2
26 7 2 2 6
27 8 2 2 3
28 9 2 2 6
29 6 2 3 3
30 7 2 3 2
31 8 2 3 3
32 9 2 3 6
33 6 2 4 2
34 7 2 4 3
35 8 2 4 3
36 9 2 4 4

 

[1] – 言語Rによる分散分析

 

ANOVA君で分析するためのデータの整形

ANOVA君では、1対象者を1行にまとめてデータを記述するワイド形式と、1行に一つのデータ（従属変数）を記述するロング形式の両方の整形方法に対応しています[1]。ワイド形式とロング形式のそれぞれの利点はこちら[1]のページに詳しく記載されています。

一元配置分散分析の記事ではワイド形式のデータを扱いましたので、ここではロング形式のデータを扱ってみることにします。

ロング形式のデータを作る際には、あらかじめ指定された順番で変数を並べたdata.frameを作成しておく必要があります。

一番左から
被験者番号、被験者間（繰り返しのない、対応のない）要因、被験者内（繰り返しのある、対応のある）要因、従属変数

です。

[1] 井関龍太のページ  – ANOVA君/より高度な入力方式

 

交互作用の確認

Rには交互作用を確認するためのグラフを作成するinteraction.plot関数が用意されています。

R Console 
> interaction.plot(SPFp.q$a, SPFp.q$b, SPFp.q$result) # interaction.plot(要因a, 要因b, 従属変数)の順に記述。

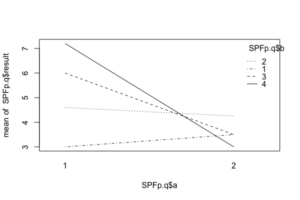
グラフが交差しているので交互作用があるようです。

 

ANOVA君の実行

詳細はANOVA君のページ[1]を参照してください。
こちらは蛍光ペン（黄）anovakun(データ, “要因計画の型”, 各要因の水準数をデータの並び順に入力, long=T)

と記述します。

要因計画の型は、AsBなどと記述します。sの左側は被験者間要因、sの右側は被験者内要因をデータフレームに配置した順番に書いていきます。AsBなら、被験者間要因である（繰り返しのない、対応のない）要因A、と被験者内要因である（繰り返しのある、対応のある）要因Bの2要因から構成される二元配置分散分析になります。sABなら2つとも被験者内要因である二元配置分散分析、ABsなら2つとも被験者間要因である二元配置分散分析ということになります。

・data.frameではそれぞれの要因に変数名を付けていてもanovakun関数にはA、B、C…の順にアルファベットを指定します。

・要因計画の型は、””でくくります（私はよく忘れて、あれ？となります）。

R Console 
> anovakun(SPFp.q, "AsB", 2, 4, long=TRUE)

[ AsB-Type Design ]

This output was generated by anovakun 4.8.2 under R version 3.4.2.
It was executed on Tue Apr 24 09:04:55 2018.

 
<< DESCRIPTIVE STATISTICS >> # 要因a、bの記述統計。

------------------------------
  a   b   n    Mean    S.D. 
------------------------------
  1   1   5  3.0000  1.4142 
  1   2   5  4.6000  1.5166 
  1   3   5  6.0000  1.4142 
  1   4   5  7.2000  1.4832 
  2   1   4  3.5000  1.2910 
  2   2   4  4.2500  2.0616 
  2   3   4  3.5000  1.7321 
  2   4   4  3.0000  0.8165 
------------------------------


<< SPHERICITY INDICES >> # 球面性の検定。被験者内要因に対して分散が等しいか検定する。p>0.05なら分散が等しいと判断。

== Mendoza's Multisample Sphericity Test and Epsilons == # 球面性の検定の方法はMauchlyの方法が有名なようですが、anova君ではMendozaの方法がデフォ。こっちの方が何か有利らしい。分散が等しくなかった場合は自由度が調整され、その後の計算が行われる。自由度の調整も色々あるみたいで、オプションで選択できる。

-------------------------------------------------------------------------
 Effect  Lambda  approx.Chi  df      p         LB     GG     HF     CM 
-------------------------------------------------------------------------
      b  0.0554      3.8012  11 0.9759 ns  0.3333 0.7903 1.2218 0.9637 
-------------------------------------------------------------------------
                              LB = lower.bound, GG = Greenhouse-Geisser
                             HF = Huynh-Feldt-Lecoutre, CM = Chi-Muller


<< ANOVA TABLE >> # 分散分析表

== This data is UNBALANCED!! ==
== Type III SS is applied. == # SSは「平方和」こと。要因のデータ数が異なる場合、平方和の推定を行うのだが、その際の方法がTypeI〜IVなどあるとか[1]。

-----------------------------------------------------------
    Source        SS  df       MS  F-ratio  p-value      # ソース、平方和、自由度、平均平方、F比、P値
-----------------------------------------------------------
         a   23.8347   1  23.8347   4.4625   0.0725 +    
     s x a   37.3875   7   5.3411                        
-----------------------------------------------------------
         b   17.1931   3   5.7310   4.7452   0.0111 *    
     a x b   30.0819   3  10.0273   8.3026   0.0008 ***  
 s x a x b   25.3625  21   1.2077                        
-----------------------------------------------------------
     Total  138.9722  35   3.9706                        
               +p < .10, *p < .05, **p < .01, ***p < .001


<< POST ANALYSES >> # 事後検定。以下、有意差があった組み合わせの多重比較検定を行って行く。

< MULTIPLE COMPARISON for "b" > # 要因bにおける多重比較検定。

== Shaffer's Modified Sequentially Rejective Bonferroni Procedure ==
== The factor < b > is analysed as dependent means. == 
== Alpha level is 0.05. == 
 
--------------------------
  b   n    Mean    S.D. 
--------------------------
  1   9  3.2500  1.3017 
  2   9  4.4250  1.6667 
  3   9  4.7500  1.9650 
  4   9  5.1000  2.5000 
--------------------------

-------------------------------------------------------
 Pair     Diff  t-value  df       p   adj.p          # ペア、差、t値、自由度、p値、Bonferroni調整p値
-------------------------------------------------------
  1-4  -1.8500   3.4589   7  0.0106  0.0634  1 = 4   
  1-2  -1.1750   2.9383   7  0.0218  0.0653  1 = 2   
  1-3  -1.5000   2.5226   7  0.0397  0.1190  1 = 3   
  2-4  -0.6750   1.4256   7  0.1970  0.5911  2 = 4   
  3-4  -0.3500   0.7432   7  0.4816  0.9631  3 = 4   
  2-3  -0.3250   0.5238   7  0.6166  0.9631  2 = 3   
-------------------------------------------------------


< SIMPLE EFFECTS for "a x b" INTERACTION > 

-------------------------------------------------------------------------
 Effect  Lambda  approx.Chi  df      p         LB     GG     HF     CM 
-------------------------------------------------------------------------
 b at 1  0.3756      1.3330   5 0.9356 ns  0.3333 0.8122 2.1712 0.9382 
 b at 2  0.1703      2.0323   5 0.8673 ns  0.3333 0.5873 1.3592 0.3333 
-------------------------------------------------------------------------
                              LB = lower.bound, GG = Greenhouse-Geisser
                             HF = Huynh-Feldt-Lecoutre, CM = Chi-Muller

-----------------------------------------------------------
     Source       SS  df       MS  F-ratio  p-value      
-----------------------------------------------------------
     a at 1   0.5556   1   0.5556   0.2991   0.6014 ns   
    Er at 1  13.0000   7   1.8571                        
-----------------------------------------------------------
     a at 2   0.2722   1   0.2722   0.0868   0.7768 ns   
    Er at 2  21.9500   7   3.1357                        
-----------------------------------------------------------
     a at 3  13.8889   1  13.8889   5.7190   0.0481 *    
    Er at 3  17.0000   7   2.4286                        
-----------------------------------------------------------
     a at 4  39.2000   1  39.2000  25.4074   0.0015 **   # 要因bが4の時に要因aの2水準の間に差がある。
    Er at 4  10.8000   7   1.5429                        
-----------------------------------------------------------
     b at 1  49.2000   3  16.4000  15.3750   0.0002 ***  # 要因aが1の時に要因bの4水準の間のどこかに差がある。
 s x b at 1  12.8000  12   1.0667                        
-----------------------------------------------------------
     b at 2   3.1875   3   1.0625   0.7612   0.5436 ns   
 s x b at 2  12.5625   9   1.3958                        
-----------------------------------------------------------
               +p < .10, *p < .05, **p < .01, ***p < .001


< MULTIPLE COMPARISON for "b at 1" > # 「要因bが4の時に要因aの2水準の間に差がある」に対する多重比較検定。

== Shaffer's Modified Sequentially Rejective Bonferroni Procedure ==
== The factor < b at 1 > is analysed as dependent means. == 
== Alpha level is 0.05. == 
 
-------------------------------------------------------
 Pair     Diff  t-value  df       p   adj.p          
-------------------------------------------------------
  1-4  -4.2000   5.2500   4  0.0063  0.0378  1 < 4 * 
  1-3  -3.0000   4.7434   4  0.0090  0.0378  1 < 3 * 
  2-4  -2.6000   4.3333   4  0.0123  0.0378  2 < 4 * 
  1-2  -1.6000   3.1379   4  0.0349  0.1048  1 = 2   
  2-3  -1.4000   2.0642   4  0.1079  0.2159  2 = 3   
  3-4  -1.2000   1.8091   4  0.1447  0.2159  3 = 4   
-------------------------------------------------------

output is over --------------------///

 

[1] 井関龍太のページ  – ANOVA君/より高度な入力方式

[2] 井関龍太のページ  – ANOVA君/平方和のタイプ

 

Print Friendly, PDF & Email

コメントを残す

メールアドレスが公開されることはありません。 ※ が付いている欄は必須項目です

このサイトはスパムを低減するために Akismet を使っています。コメントデータの処理方法の詳細はこちらをご覧ください。

前の記事

二項ロジスティック回帰分析

次の記事

リスク比とオッズ比